Protective Collar

Definition

A Protective Collar is an option strategy that involves both the underlying stock and two option contracts. The trader buys (or already owns) a stock, then buys an out-the-money put option and sells an out-the-money call option.  It is similar to the covered call strategy but with the purchase of an additional put option. This strategy is employed if the trader is writing covered calls but wishes to protect himself from an unexpected drop in the price of the underlying security. As a tradeoff for loss-protection, the profit is limited compared with the Covered Call strategy.

# Protective Collar
price = np.arange(700,950,1)
# assume at time 0, the price of the undelying stock is 830
k_otm_put = 800 # the strike price of OTM put
k_otm_call = 860 # the strike price of OTM call
premium_otm_put = 6 # the premium of OTM put
premium_otm_call = 2 # the premium of OTM call
# payoff for the long put position
payoff_long_put = [max(-premium_otm_put, k_otm_put-i-premium_otm_put) for i in price]
# payoff for the short call position
payoff_short_call = [min(premium_otm_call, -(i-k_otm_call-premium_otm_call)) for i in price]
# payoff for the underlying stock
payoff_stock = price - 830
# payoff for the Protective Collar Strategy
payoff = np.sum([payoff_long_put,payoff_short_call,payoff_stock], axis=0)
plt.figure(figsize=(20,15))
plt.plot(price, payoff_long_put, label = 'Long Put',linestyle='--')
plt.plot(price, payoff_short_call, label = 'Short Call',linestyle='--')
plt.plot(price, payoff_stock, label = 'Underlying Stock',linestyle='--')
plt.plot(price, payoff, label = 'Protective Collar',c='black')
plt.legend(fontsize = 20)
plt.xlabel('Stock Price at Expiry',fontsize = 15)
plt.ylabel('payoff',fontsize = 15)
plt.title('Protective Collar Strategy - Payoff',fontsize = 20)
plt.grid(True)

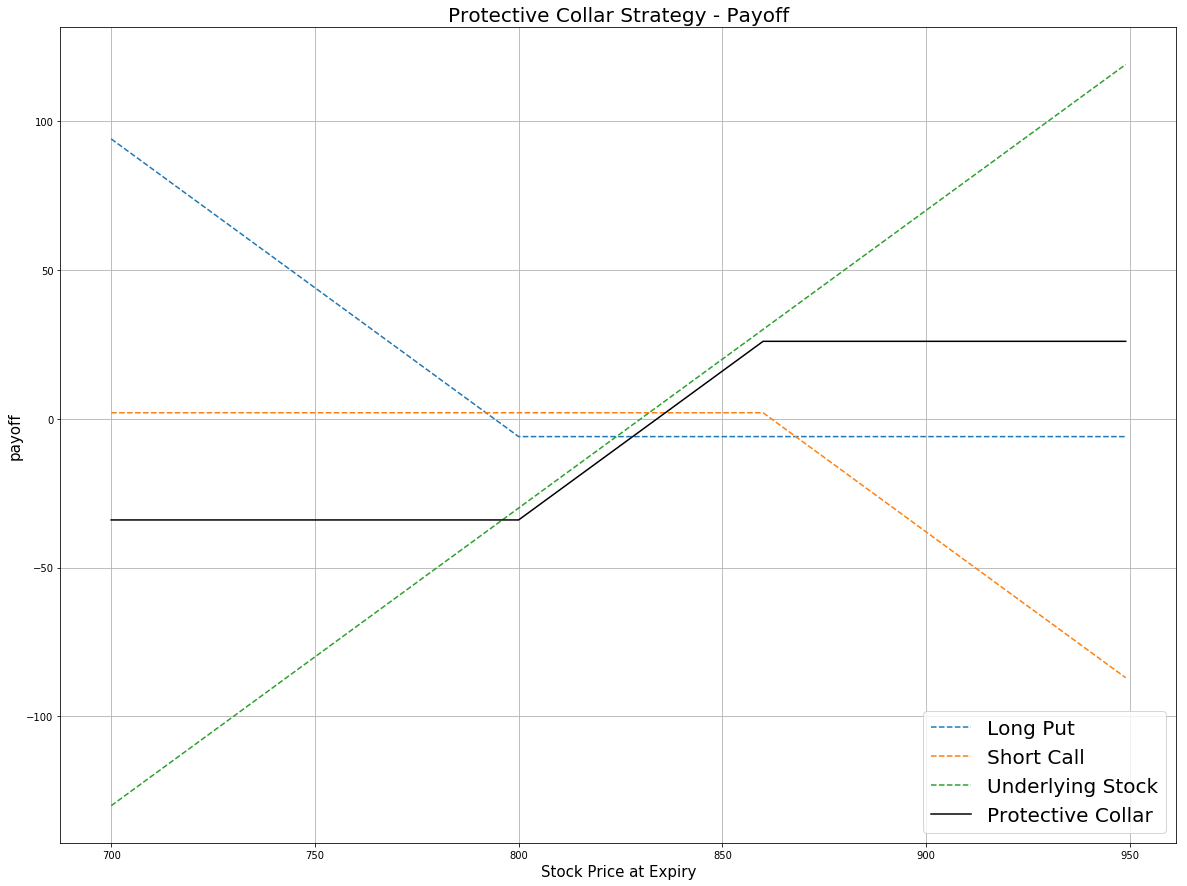
According to the payoff plot, the maximum profit is the strike price of short call minus the purchase price of the underlying asset plus the net credit from the premium. It occurs when the underlying price is beyond the strike price of the short call option. The maximum loss is the purchase price of the underlying asset minus the strike price of the long put minus the net credit from the premium. It occurs when the stock price is below the strike price of the long put. It is a strategy with both limited risk and limited profit.

Implementation

Step 1: Initialize your algorithm by setting the start date, end date and cash. Then implement the coarse selection of options contracts.

def Initialize(self):
    self.SetStartDate(2017, 4, 1)
    self.SetEndDate(2017, 5, 30)
    self.SetCash(1000000)
    equity = self.AddEquity("GOOG", Resolution.Minute)
    option = self.AddOption("GOOG", Resolution.Minute)
    self.symbol = option.Symbol
    # set our strike/expiry filter for this option chain
    option.SetFilter(-10, +10, timedelta(0), timedelta(30))
    # use the underlying equity as the benchmark
    self.SetBenchmark(equity.Symbol)

Step 2: Choose the expiration date for your options traded and break the options into the call and put contracts. The choice of expiration date depends on the holding period of stocks in your portfolio.

def TradeOptions(self,optionchain):
    for i in optionchain:
    if i.Key != self.symbol: continue
    chain = i.Value
    # choose the furthest expiration date within 30 days from now on
    expiry = sorted(chain, key = lambda x: x.Expiry)[-1]
    # filter the call options contracts
    call = [x for x in chain if x.Right == 0 and x.Expiry == expiry]
    # filter the put options contracts
    put = [x for x in chain if x.Right == 1 and x.Expiry == expiry]

Step 3: Choose the deep in-the-money call and put options in the list and then sell the call options and buy the put options.

self.otm_call = sorted(call, key = lambda x: x.Strike)[-1]
self.otm_put = sorted(put, key = lambda x: x.Strike)[0]
if (self.otm_call is None) or (self.otm_put is None): continue
self.Sell(self.otm_call.Symbol, 1) # sell the OTM call
self.Buy(self.otm_put.Symbol, 1) # buy the OTM put

Step 4: In OnData, if there are no assets in our portfolio, we buy the undelying stock. After that, we trade the options written on the same number of shares of underlying asset (one option contracts equals 100 undelying shares).

def OnData(self,slice):
    optionchain = slice.OptionChains
    for i in slice.OptionChains:
    if i.Key != self.symbol: continue
    chains = i.Value
    contract_list = [x for x in chains]
    if (slice.OptionChains.Count == 0) or (len(contract_list) == 0): return
    # if you don't hold options and stocks, buy the stocks and trade the options
    if not self.Portfolio.Invested:
    self.Buy("GOOG",100)     # buy 100 shares of the underlying stock
    self.TradeOptions(optionchain)   # sell OTM call and buy OTM put

Summary

In this algorithm, at the beginning  01/04/2016, we purchased 100 GOOG shares. At the same time, we purchased a $715 put at $6 and sells a $772.5 call at $2.45. The share price of GOOG is $739.32, which is between the strike prices of two out-the-money options. At the expiry 01/15/2016, the share price of GOOG drops to $714.32. The call option expire worthless but the put option is exercised. Then we sell 100 GOOG shares at $715. Then we hold neither option positions and stock positions.

---

---

---