One of the most important aspects of trading is risk management. Knowing when the market is going to move against you and acting before this happens is the best way to avoid large drawdowns and maximize your Sharpe ratio. The ultimate strategy is buy-low, sell-high. The trouble with this, however, is knowing when low is low and high is high. Hindsight is 20/20, but can we find a way to understand when markets are about to shift from bull to bear?
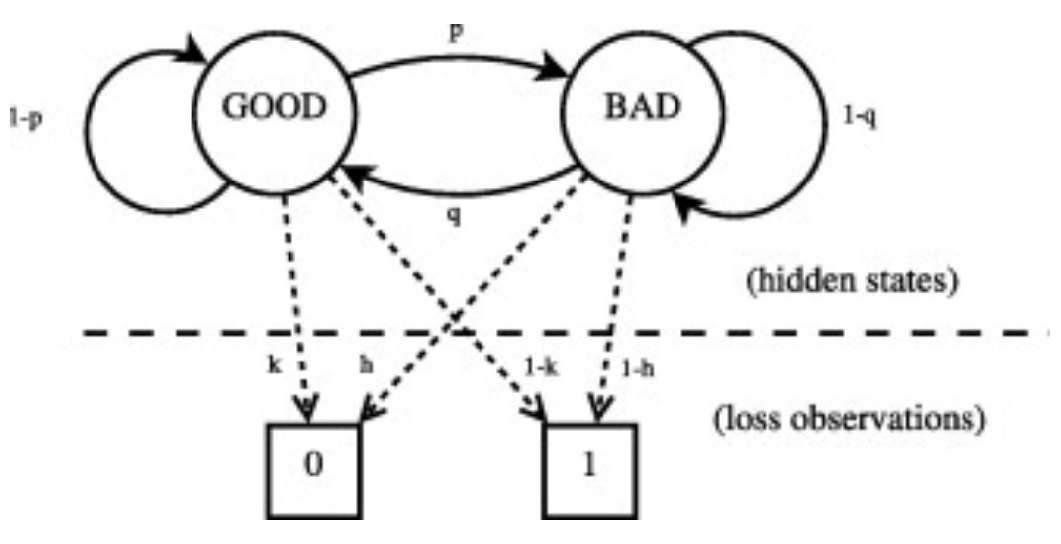
One possibility is to use a Hidden Markov Model (HMM). These are Markov models where the system is being modeled as a Markov process but whose states are unobserved, or hidden. (Briefly, a Markov process is a stochastic process where the possibility of switching to another state depends only on the current state of the model -- it is history-independent, or memoryless). In a regular Markov model, the state is observable by the user and so the only parameters are the state transition probabilities. For example, in a two-state Markov model, the user is able to know which state the system being modeled is in, and so the only model parameters to be characterized are the probabilities of attaining each state.
In an HMM, each state has transition probabilities and there are underlying latent states, but they are not directly observable. Instead, they influence the observations which are the only observable element.
As with Kalman filters, there are three main aspects of interest to us:
- Prediction - forecasting future values of the process
- Filtering - estimating the current state of the model
- Smoothing - estimating past states of the model
The salient feature here is prediction as our ultimate goal is to predict the market state. To experiment with this, we used the research notebook to get historical data for SPY and fit a Gaussian, two-state Hidden Markov Model to the data. We built a few functions to build, fit, and predict from our Gaussian HMM.
from HMM import *
import numpy as np
from scipy.stats import jarque_bera
symbol = qb.AddEquity('SPY', Resolution.Daily).Symbol
# Fetch history and returns
history = qb.History(symbol, 500, Resolution.Hour)
returns = history.close.pct_change().dropna()
# Define Hidden Markov Model functions
def CreateHMM(algorithm, symbol):
history = algorithm.History([symbol], 900, Resolution.Daily)
returns = np.array(history.loc[symbol].close.pct_change().dropna())
# Reshape returns
returns = np.array(returns).reshape((len(returns),1))
# Initialize Gaussian Hidden Markov Model
model = GaussianHMM(n_components=2, covariance_type="full", n_iter=1000).fit(returns)
print(model.score(returns))
return model
def PlotStates(algorithm, symbol, model):
history = algorithm.History([symbol], 900, Resolution.Daily).loc[symbol]
returns = history.close.pct_change().dropna()
hidden_states = model.predict(np.array(returns).reshape((len(returns),1)))
hidden_states = pd.Series(hidden_states, index = returns.index)
hidden_states.name = 'hidden'
bull = hidden_states.loc[hidden_states.values == 0]
bear = hidden_states.loc[hidden_states.values == 1]
plt.figure()
ax = plt.gca()
ax.plot(bull.index, bull.values, ".", linestyle='none', c = 'b', label = "Bull Market")
ax.plot(bear.index, bear.values, ".", linestyle='none', c = 'r', label = "Bear Market")
plt.title('Hidden States')
ax.legend()
plt.show()
df = history.join(hidden_states, how = 'inner')
df = df[['close', 'hidden']]
up = pd.Series()
down = pd.Series()
mid = pd.Series()
for tuple in df.itertuples():
if tuple.hidden == 0:
x = pd.Series(tuple.close, index = [tuple.Index])
up = up.append(x)
else:
x = pd.Series(tuple.close, index = [tuple.Index])
down = down.append(x)
up = up.sort_index()
down = down.sort_index()
plt.figure()
ax = plt.gca()
ax.plot(up.index, up.values, ".", linestyle='none', c = 'b', label = "Bull Market")
ax.plot(down.index, down.values, ".", linestyle='none', c = 'r', label = "Bear Market")
plt.title('SPY')
ax.legend()
plt.show()
# Build the model and plot good/bad regime states
model = CreateHMM(qb, symbol)
PlotStates(qb, symbol, model)As we can see, the HMM we fit with SPY returns data does a reasonably good job of detecting bear markets bull markets. To apply this in a model, we decided to use it as a way to manage risk in the algorithm developed using stationarity and z-scores. The basic mean-reversion strategy remains, but instead, we add the condition to enter a position that the security must be in a bull-state, and all positions are exited and no trading happens during a bear-state.
(The specific application of an HMM to SPY returns and as use in risk management is thanks in part to articles on HMM and trading found here and here.)
To do this, we initialize and fit a Gaussian, two-state HMM model for each security when they are added to the universe.
def OnSecuritiesChanged(self, changes):
symbols = [x.Symbol for x in changes.AddedSecurities]
# Build model for each symbol
for symbol in symbols:
self.models[symbol] = CreateHMM(self, symbol)Every day, we run our tests for stationarity, get z-scores, make our state-prediction, and then iterate over all of the symbols and apply our trading logic.
def GenerateInsights(self):
insights = []
qb = self
symbols = [x.Symbol for x in qb.ActiveSecurities.Values]
# Copy and paste from research notebook
# -----------------------------------------------------------------------------
# Fetch history
history = qb.History(symbols, 500, Resolution.Hour)
# Convert to returns
returns = history.unstack(level = 1).close.transpose().pct_change().dropna()
# Test for stationarity
stationarity = TestStationartiy(returns)
# Get z-scores
z_scores = GetZScores(returns)
# -----------------------------------------------------------------------------
insights = []
# Iterate over symbols
for symbol, value in stationarity.iteritems():
# Only emit Insights for those whose returns exhibit stationary behavior
if value:
# Get Hidden Markov model
model = self.CheckForHMM(symbol)
# Predict current state
state_prediction = PredictState(self, model, symbol)
# Get most recent z_score
z_score = z_scores[symbol].tail(1).values[0]
# Determine if we want to invest or not
if (z_score < -1) and (state_prediction == 0):
insights.append(Insight.Price(symbol, timedelta(1), InsightDirection.Up))
elif z_score > 1:
if self.Portfolio[symbol].Invested:
insights.append(Insight.Price(symbol, timedelta(1), InsightDirection.Flat))
elif self.Portfolio[symbol].Invested and (state_prediction == 1):
insights.append(Insight.Price(symbol, timedelta(1), InsightDirection.Flat))
self.EmitInsights(insights)Finally, we re-fit the models every 30 days.
def RefitModels(self):
for symbol, model in self.models.items():
RefitModel(self, symbol, model)All of this is done using an Immediate Execution Model, Equal Weighting Portfolio Construction Model, and the Liquid ETF Universe.
def Initialize(self):
self.SetStartDate(2019, 1, 1) # Set Start Date
self.SetCash(100000) # Set Strategy Cash
self.SetBrokerageModel(AlphaStreamsBrokerageModel())
self.SetExecution(ImmediateExecutionModel())
self.SetPortfolioConstruction(EqualWeightingPortfolioConstructionModel())
self.SetUniverseSelection(LiquidETFUniverse())
self.models = {}
self.AddEquity('GLD')
self.Schedule.On(self.DateRules.EveryDay('GLD'), self.TimeRules.AfterMarketOpen('GLD', 5), self.GenerateInsights)
self.Schedule.On(self.DateRules.MonthStart('GLD'), self.TimeRules.At(19,0), self.RefitModels)As can be seen in the attached backtest, using Hidden Markov Models to detect optimal market conditions actually decreased our algorithm's performance vs the algorithm using just stationarity tests and z-scores, but this doesn't mean that we shouldn't continue to experiment with them. Perhaps a two-state HMM was great at predicting bear/bull states for index ETFs but not for sector ETFs and applying the way we did here was a mistake. Either way, detecting bear/bull market states are hardly the only application of Hidden Markov Models in finance. These can be used to detect when time-series attain various states with respect to all sorts of statistical properties, and their application can be in risk-management, portfolio construction, execution, or determining optimal trading rules.
Have fun and good luck!



















Pi..R
Thank you very much for sharing Jack, super interesting! Would it be possible to provide this implementation (or any of the other ones you have been sharing recently) in C#?
It would probably be too much work to have to rewrite each of those manually, but maybe you have a script or something that is able to convert from Python to C# automatically?? I am still very new to coding and started to learn C# as most of the ressources available for Quantconnect were in that language a year ago or so, but it seems like those days most educational things on the platform are being done in Python.
Ivan Baev
Thank you for this beautiful example. Before I've thought Markov's models don't work in real life trading, regarding it as simply an academic topic. Enjoyed reading this.
Taylor Robertson
I cloned this model as-is and ran it twice. I got different results. The attached backtest has 3.9% total return. The second iteration, using the exact same code, had 1.7% total return and a very different path to get there. Can you explain why that is?
Jack Simonson
Hi Taylor,
In the HMM model from the hmmlearn module that we use, there is a random_state variable we left un-set. Sit it isn't defined, it won't be the same each run and therefore the results can differ between backtests. However, if you explicitly declare it, you should get the same results each time.
For example, you could do this in the HMM.py file
GaussianHMM(n_components=2, covariance_type="full", n_iter=1000, random_state = 100).fit(returns)Taylor Robertson
Is there a reason from the mathematical theory behind HMM that it should be left to randomize? What risk am I introducing by fixing the seed number for the random state to a constant? Thanks for the help as this is new to me, but looks very powerful.
Jack Simonson
The random element is done in the K-Means clustering. In the context of the Gaussian HMM, it is essentially randomly sampling the inputs to try to determine the data that belong to the different states. There is no real risk in fixing the random state seed. Rather, fixing it will allow yourself or other users to replicate your results.
There is a lot of good information out there, and the source code to the hmmlearn and sklearn libraries are helpful. I'd recommend checking out the following links:
https://scikit-learn.org/stable/modules/clustering.html#k-means
https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
https://hmmlearn.readthedocs.io/en/latest/api.html
Derek Melchin
Hi Chris,
In the case of backtesting, since LEAN doesn't allow look-ahead bias, the data is already split in some sense. The model is trained on historical data, then tested on future unseen data. Splitting the data would be more appropriate in the research environment to ensure we don't train and test the model on the same data.
Best,
Derek Melchin
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
Carsten
Hi Jack,
very interesting, I was trying something similar, I got with a support vector machine promising results. Unfortunately I was very slow.
I was thinking to use something like this to switch between strategies.
How would one do this with the quantconnct framework? Is there a possibility to generate a signal and than according to the signal run two alphamodel and switch one on or off?
Thanks Carsten
Shile Wen
Hi Carsten,
We can determine which alpha model's Insights to take inside the Portfolio Construction Model by checking the class of where the Insight came from using Insight.SourceModel.
Best,
Shile Wen
Carsten
Shile Wen, thanks I'm looking into that. In a first step I manipulated the insights, but it would be way better to do this in the Portfolio Construction Model as you suggested. To transfer the signal into the Portfolio Construction Model (actually im sending it to the Alpha model) i'm using a ObjectStore object. If I just would use a simple variable True/Fals or a single float, coulds this be done some how with a "global" variable?
Now the more tricky question. I would like to get the past theoretical returns from AlphaModel A and AlphaModel B. They should not be invested, i just would like to use them as a signal and than into a HMM. This should then gnerate the signal for the Portfolio Construction Model. How would you do that?
Many thanks Carsten
Meneo
Hi Jack,
Great post! The idea, backed by the research looks promising.
However I find a disconnect between the backtests & the research.
I played around a bit, working with only SPY.
Here are my challenges -
1. You use pct_change on the close for training the model, but use close/price to predict. Is this right?
2. The model predictions (HMM states) as seen in the research book looks good & logical.
However same model or model trained on same data has very different predictions when used in backtesting.
3. I modified the predict code to use pct_change instead of the close price.
Still, the HMM plots in the backtest don't match the research.
I also tried saving the trained model in the research book and using it in backtest via objectstore.
Again they don't match. This is very puzzling to me.
Have you verified the correctness of the prediction in the backtest - whether or not it's same/similar to
research book predictions ?
Please see plots for the HMM states in the backtest. It doesn't match the plots in the research at all.
Attached is a clone of yours with no trades/insights + prediction based on pct_change + plots for HMM states +
research & backtest trained on same set of data.
Thanks
PS: I am not an expert in ML or python. So if I have misunderstood the code / ML logic, please correct me
Carsten
Menno Dreischor try sklearn OneClassSVM, it gave me slighty better results(but much slower). I was playing around with HMM and the finding was, if you run it over the whole period, it looks like you could use it to time the SPY/Market. if it tried to run it with an array of even up to 4000 past days, the results are not anymore there, meaning you can't time the market anymore....i was using probably returns. For the full period my results are looking pretty much like the ones abouve. But I just did this for an evening, probably I need to spend more time on that.
Meneo
Carsten Thanks, will try out the OneClassSVM model.
The main concern for my post though is why doesn't the same model produce similar results in the backtest & the research?
I even tried saving (in research) & reusing the trained HMM model in the backest. This should predict exact same HMM states as in research, but it didn't!
Which leads me to believe there's something wrong with Python implementation or with Quantconnect.
What am I missing?
Jack Simonson
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
To unlock posting to the community forums please complete at least 30% of Boot Camp.
You can continue your Boot Camp training progress from the terminal. We hope to see you in the community soon!