Meta Analysis

To get the results of a live algorithm, call the ReadLiveAlgorithmread_live_algorithm method with the project Id and deployment ID.

#load "../Initialize.csx"
#load "../QuantConnect.csx"

using QuantConnect;
using QuantConnect.Api;

var liveAlgorithm = api.ReadLiveAlgorithm(projectId, deployId);

live_algorithm = api.read_live_algorithm(project_id, deploy_id)

The following table provides links to documentation that explains how to get the project Id and deployment Id, depending on the platform you use:

The ReadLiveAlgorithmread_live_algorithm method returns a LiveAlgorithmResults object, which have the following attributes:

Reconciliation is a way to quantify the difference between an algorithm's live performance and its out-of-sample (OOS) performance (a backtest run over the live deployment period).

Seeing the difference between live performance and OOS performance gives you a way to determine if the algorithm is making unrealistic assumptions, exploiting data differences, or merely exhibiting behavior that is impractical or impossible in live trading.

A perfectly reconciled algorithm has an exact overlap between its live equity and OOS backtest curves. Any deviation means that the performance of the algorithm has differed for some reason. Several factors can contribute to this, often stemming from the algorithm design.

Reconciliation is scored using two metrics: returns correlation and dynamic time warping (DTW) distance.

What is DTW Distance?

Dynamic Time Warp (DTW) Distance quantifies the difference between two time-series. It is an algorithm that measures the shortest path between the points of two time-series. It uses Euclidean distance as a measurement of point-to-point distance and returns an overall measurement of the distance on the scale of the initial time-series values. We apply DTW to the returns curve of the live and OOS performance, so the DTW distance measurement is on the scale of percent returns.

For the reasons outlined in our research notebook on the topic (linked below), QuantConnect annualizes the daily DTW. An annualized distance provides a user with a measurement of the annual difference in the magnitude of returns between the two curves. A perfect score is 0, meaning the returns for each day were precisely the same. A DTW score of 0 is nearly impossible to achieve, and we consider anything below 0.2 to be a decent score. A distance of 0.2 means the returns between an algorithm's live and OOS performance deviated by 20% over a year.

What is Returns Correlation?

Returns correlation is the simple Pearson correlation between the live and OOS returns. Correlation gives us a rudimentary understanding of how the returns move together. Do they trend up and down at the same time? Do they deviate in direction or timing?

An algorithm's returns correlation should be as close to 1 as possible. We consider a good score to be 0.8 or above, meaning that there is a strong positive correlation. This indicates that the returns move together most of the time and that for any given return you see from one of the curves, the other curve usually has a similar direction return (positive or negative).

Why Do We Need Both DTW and Returns Correlation?

Each measurement provides insight into distinct elements of time-series similarity, but neither measurement alone gives us the whole picture. Returns correlation tells us whether or not the live and OOS returns move together, but it doesn't account for the possible differences in the magnitude of the returns. DTW distance measures the difference in magnitude of returns but provides no insight into whether or not the returns move in the same direction. It is possible for there to be two cases of equity curve similarity where both pairs have the same DTW distance, but one has perfectly negatively correlated returns, and the other has a perfectly positive correlation. Similarly, it is possible for two pairs of equity curves to each have perfect correlation but substantially different DTW distance. Having both measurements provides us with a more comprehensive understanding of the actual similarity between live and OOS performance. We outline several interesting cases and go into more depth on the topic of reconciliation in research we have published.

Follow these steps to plot the daily order fills of a live algorithm:

1. Get the live trading orders.

orders = api.read_live_orders(project_id)

The following table provides links to documentation that explains how to get the project Id, depending on the platform you use:

Platform	Project Id
Cloud Platform	Get Project Id
Local Platform	Get Project Id
CLI	Get Project Id

By default, the orders with an ID between 0 and 100. To get orders with an ID greater than 100, pass start and end arguments to the ReadLiveOrdersread_live_orders method. Note that end - start must be less than 100.

orders = api.read_live_orders(project_id, 100, 150)

The ReadLiveOrdersread_live_orders method returns a list of Order objects, which have the following properties:

2. Organize the trade times and prices for each security into a dictionary.

   class OrderData:
       def __init__(self):
           self.buy_fill_times = []
           self.buy_fill_prices = []
           self.sell_fill_times = []
           self.sell_fill_prices = []
   
   order_data_by_symbol = {}
   for order in [x.order for x in orders]:
       if order.symbol not in order_data_by_symbol:
           order_data_by_symbol[order.symbol] = OrderData()
       order_data = order_data_by_symbol[order.symbol]
       is_buy = order.quantity > 0
       (order_data.buy_fill_times if is_buy else order_data.sell_fill_times).append(order.last_fill_time.date())
       (order_data.buy_fill_prices if is_buy else order_data.sell_fill_prices).append(order.price)

3. Get the price history of each security you traded.

   qb = QuantBook()
   start_date = datetime.max.date()
   end_date = datetime.min.date()
   for symbol, order_data in order_data_by_symbol.items():
       if order_data.buy_fill_times:
           start_date = min(start_date, min(order_data.buy_fill_times))
           end_date = max(end_date, max(order_data.buy_fill_times))
       if order_data.sell_fill_times:
           start_date = min(start_date, min(order_data.sell_fill_times))
           end_date = max(end_date, max(order_data.sell_fill_times))
   start_date -= timedelta(days=3)
   all_history = qb.history(list(order_data_by_symbol.keys()), start_date, end_date, Resolution.DAILY)

4. Create a candlestick plot for each security and annotate each plot with buy and sell markers.

   import plotly.express as px
   import plotly.graph_objects as go
   
   for symbol, order_data in order_data_by_symbol.items():
       history = all_history.loc[symbol]
   
       # Plot security price candlesticks
       candlestick = go.Candlestick(x=history.index,
                                   open=history['open'],
                                   high=history['high'],
                                   low=history['low'],
                                   close=history['close'],
                                   name='Price')
       layout = go.Layout(title=go.layout.Title(text=f'{symbol.value} Trades'),
                       xaxis_title='Date',
                       yaxis_title='Price',
                       xaxis_rangeslider_visible=False,
                       height=600)
       fig = go.Figure(data=[candlestick], layout=layout)
   
       # Plot buys
       fig.add_trace(go.Scatter(
           x=order_data.buy_fill_times,
           y=order_data.buy_fill_prices,
           marker=go.scatter.Marker(color='aqua', symbol='triangle-up', size=10),
           mode='markers',
           name='Buys',
       ))
   
       # Plot sells
       fig.add_trace(go.Scatter(
           x=order_data.sell_fill_times,
           y=order_data.sell_fill_prices,
           marker=go.scatter.Marker(color='indigo', symbol='triangle-down', size=10),
           mode='markers',
           name='Sells',
       ))
   
   fig.show()



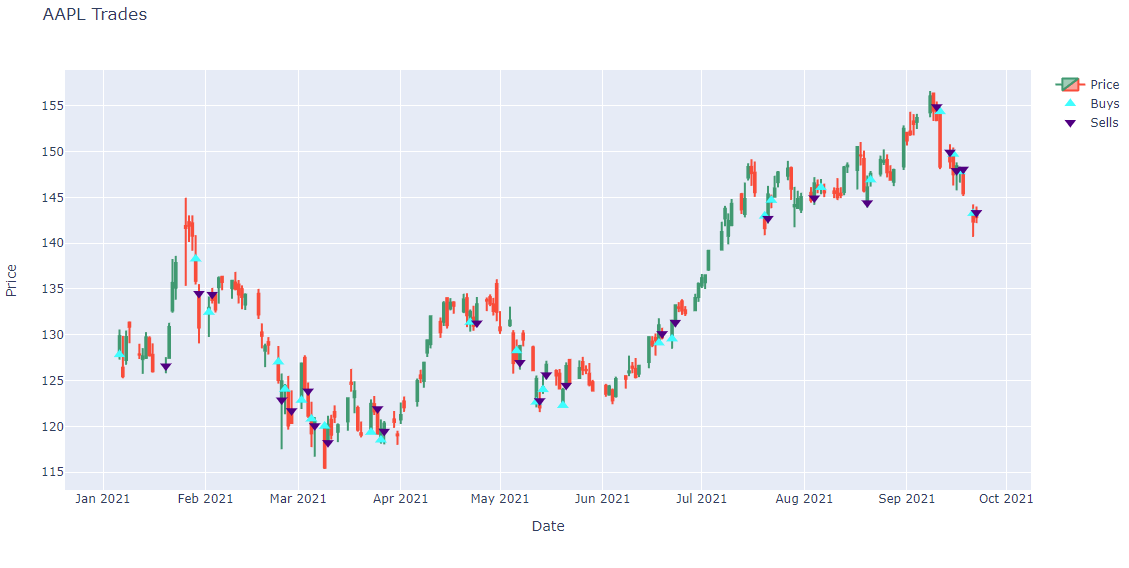
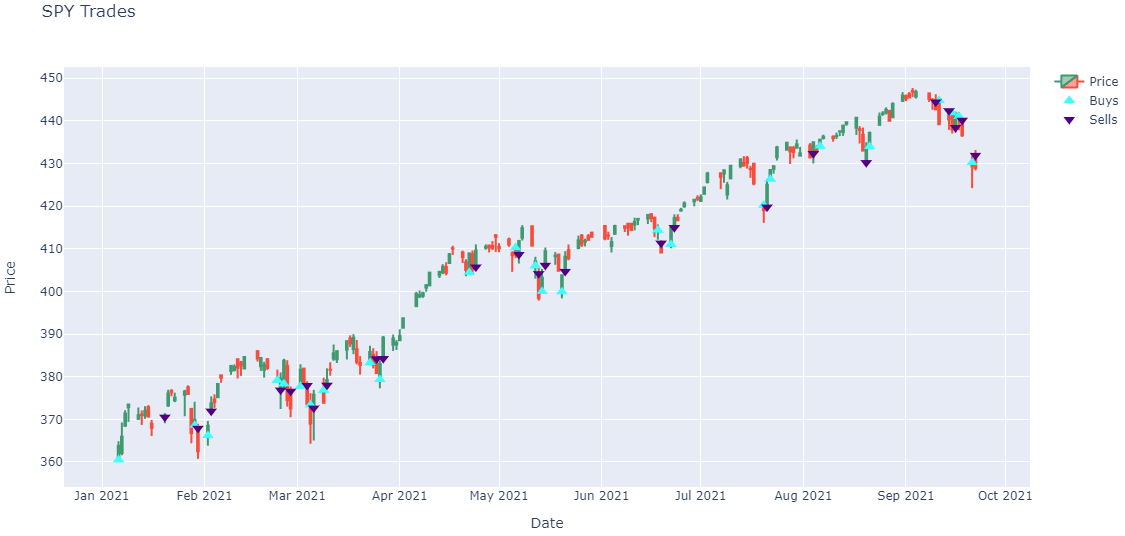
Note: The preceding plots only show the last fill of each trade. If your trade has partial fills, the plots only display the last fill.

Follow these steps to plot the equity curve, benchmark, and drawdown of a live algorithm:

1. Get the live algorithm instance.

live_algorithm = api.read_live_algorithm(project_id, deploy_id)

The following table provides links to documentation that explains how to get the project Id and deployment Id, depending on the platform you use:

Platform	Project Id	Deployment Id
Cloud Platform	Get Project Id	Get Deployment Id
Local Platform	Get Project Id	Get Deployment Id
CLI	Get Project Id

2. Get the results of the live algorithm.

results = live_algorithm.live_results.results

3. Get the "Strategy Equity", "Drawdown", and "Benchmark" Chart objects.

equity_chart = results.charts["Strategy Equity"]
drawdown_chart = results.charts["Drawdown"]
benchmark_chart = results.charts["Benchmark"]

4. Get the "Equity", "Equity Drawdown", and "Benchmark" Series from the preceding charts.

equity = equity_chart.series["Equity"].values
drawdown = drawdown_chart.series["Equity Drawdown"].values
benchmark = benchmark_chart.series["Benchmark"].values

5. Create a pandas.DataFrame from the series values.

df = pd.DataFrame({
    "Equity": pd.Series({value.TIME: value.CLOSE for value in equity}),
    "Drawdown": pd.Series({value.TIME: value.Y for value in drawdown}),
    "Benchmark": pd.Series({value.TIME: value.Y for value in benchmark})
}).ffill()

6. Plot the performance chart.

# Create subplots to plot series on same/different plots
fig, ax = plt.subplots(2, 1, figsize=(12, 12), sharex=True, gridspec_kw={'height_ratios': [2, 1]})

# Plot the equity curve
ax[0].plot(df.index, df["Equity"])
ax[0].set_title("Strategy Equity Curve")
ax[0].set_ylabel("Portfolio Value ($)")

# Plot the benchmark on the same plot, scale by using another y-axis
ax2 = ax[0].twinx()
ax2.plot(df.index, df["Benchmark"], color="grey")
ax2.set_ylabel("Benchmark Price ($)", color="grey")

# Plot the drawdown on another plot
ax[1].plot(df.index, df["Drawdown"], color="red")
ax[1].set_title("Drawdown")
ax[1].set_xlabel("Time")
ax[1].set_ylabel("%")

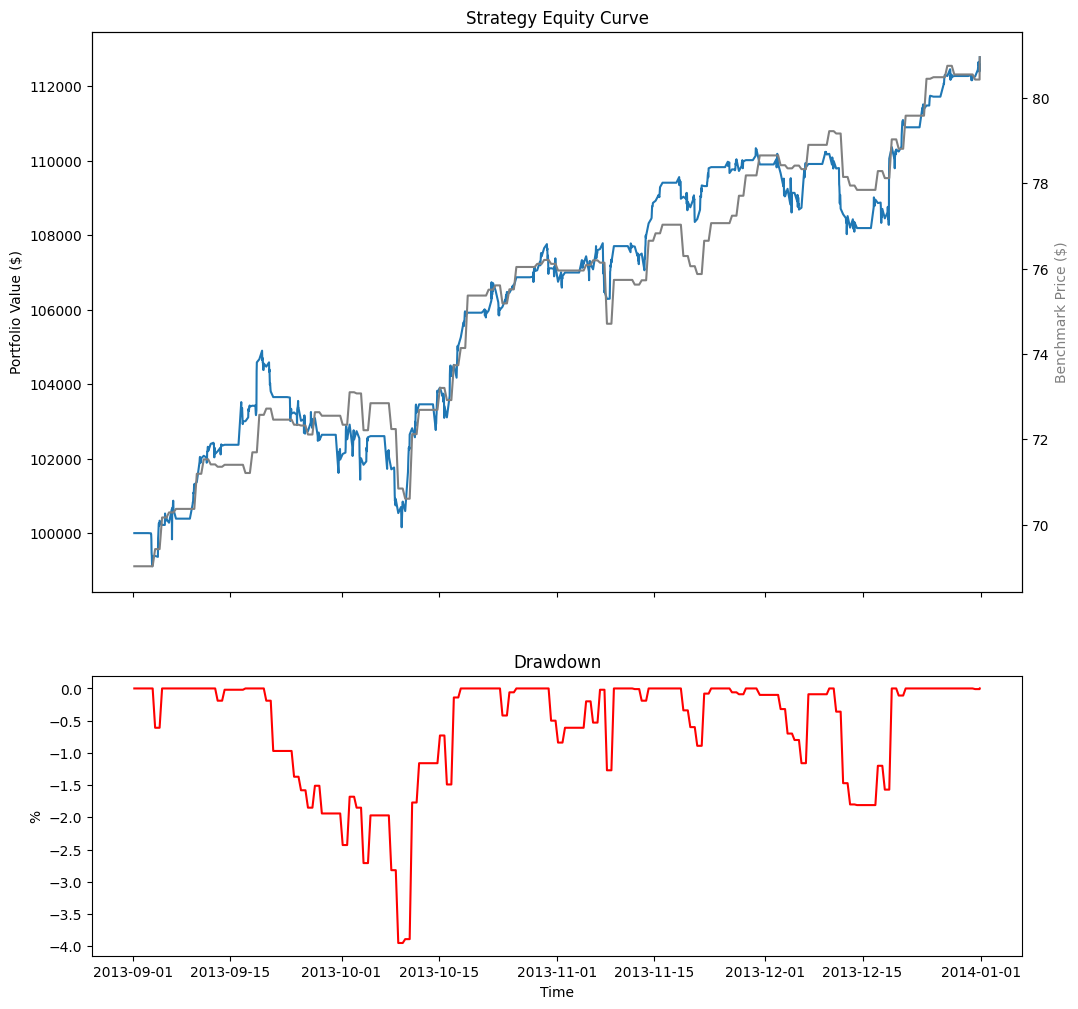
The following table shows all the chart series you can plot: