Option Strategies

Covered Call

Introduction

A Covered Call consists of a long position in a stock and a short position in call Options for the same amount of stock. Covered calls aim to profit from the Option premium by selling calls written on the stock you already own. At any time for American Options or at expiration for European Options, if the stock moves below the strike price, you keep the premium and still maintain the underlying Equity position. If the underlying price moves above the strike, the Option buyer can exercise the Options contract, which means you sell your stock at the strike price and keep the premium. Another risk of a covered call comes from the long stock position, which can drop in value.

Implementation

Follow these steps to implement the covered call strategy:

  1. In the Initializeinitialize method, set the start date, end date, starting cash, and Options universe.
    2. private Symbol _symbol;

public override void Initialize()
{
    SetStartDate(2014, 1, 1);
    SetEndDate(2014, 3, 1);
    SetCash(100000);

    UniverseSettings.Asynchronous = true;
    var option = AddOption("IBM");
    _symbol = option.Symbol;
    option.SetFilter(universe => universe.IncludeWeeklys().NakedCall(30, 0));
}
    def initialize(self) -> None:
    self.set_start_date(2014, 1, 1)
    self.set_end_date(2014, 3, 1)
    self.set_cash(100000)

    self.universe_settings.asynchronous = True
    option = self.add_option("IBM")
    self._symbol = option.symbol
    option.set_filter(lambda universe: universe.include_weeklys().naked_call(30, 0))

    The NakedCallnaked_call filter narrows the universe down to just the one contract you need to form a covered call.

  2. In the OnDataon_data method, select the Option contract.
    3. public override void OnData(Slice slice)
{
    if (Portfolio.Invested ||
        !slice.OptionChains.TryGetValue(_symbol, out var chain))
    {
        return;
    }

    // Find ATM call with the farthest expiry
    var expiry = chain.Max(x => x.Expiry);
    var atmCall = chain
        .Where(x => x.Right == OptionRight.Call && x.Expiry == expiry)
        .OrderBy(x => Math.Abs(x.Strike - chain.Underlying.Price))
        .FirstOrDefault();
    def on_data(self, slice: Slice) -> None:
    if self.portfolio.invested:
        return

    chain = slice.option_chains.get(self._symbol)
    if not chain:
        return

    # Find ATM call with the farthest expiry
    expiry = max([x.expiry for x in chain])
    call_contracts = sorted([x for x in chain
        if x.right == OptionRight.CALL and x.expiry == expiry],
        key=lambda x: abs(chain.underlying.price - x.strike))

    if not call_contracts:
        return

    atm_call = call_contracts[0]
  3. In the OnDataon_data method, place the orders.

    4. Approach A: Call the OptionStrategies.CoveredCallOptionStrategies.covered_call method with the details of each leg and then pass the result to the Buybuy method.

    var coveredCall = OptionStrategies.CoveredCall(_symbol, atmCall.Strike, expiry);
Buy(coveredCall, 1);
    covered_call = OptionStrategies.covered_call(self._symbol, atm_call.strike, expiry)
self.buy(covered_call, 1)

    Approach B: Create a list of Leg objects and then call the Combo Market Ordercombo_market_order, Combo Limit Ordercombo_limit_order, or Combo Leg Limit Ordercombo_leg_limit_order method.

    var legs = new List<Leg>()
    {
        Leg.Create(atmCall.Symbol, -1),
        Leg.Create(chain.Underlying.Symbol, chain.Underlying.SymbolProperties.ContractMultiplier)
    };
ComboMarketOrder(legs, 1);
    legs = [
    Leg.create(atm_call.symbol, -1),
    Leg.create(chain.underlying.symbol, chain.underlying.symbol_properties.contract_multiplier)
]
self.combo_market_order(legs, 1)

Strategy Payoff

The payoff of the strategy is

$$ \begin{array}{rcll} C^{K}_T & = & (S_T - K)^{+}\\ P_T & = & (S_T - S_0 + C^{K}_0 - C^{K}_T)\times m - fee \end{array} $$ $$ \begin{array}{rcll} \textrm{where} & C^{K}_T & = & \textrm{Call value at time T}\\ & S_T & = & \textrm{Underlying asset price at time T}\\ & K & = & \textrm{Call strike price}\\ & P_T & = & \textrm{Payout total at time T}\\ & S_0 & = & \textrm{Underlying asset price when the trade opened}\\ & C^{K}_0 & = & \textrm{Call price when the trade opened (credit received)}\\ & m & = & \textrm{Contract multiplier}\\ & T & = & \textrm{Time of expiration} \end{array} $$

The following chart shows the payoff at expiration:

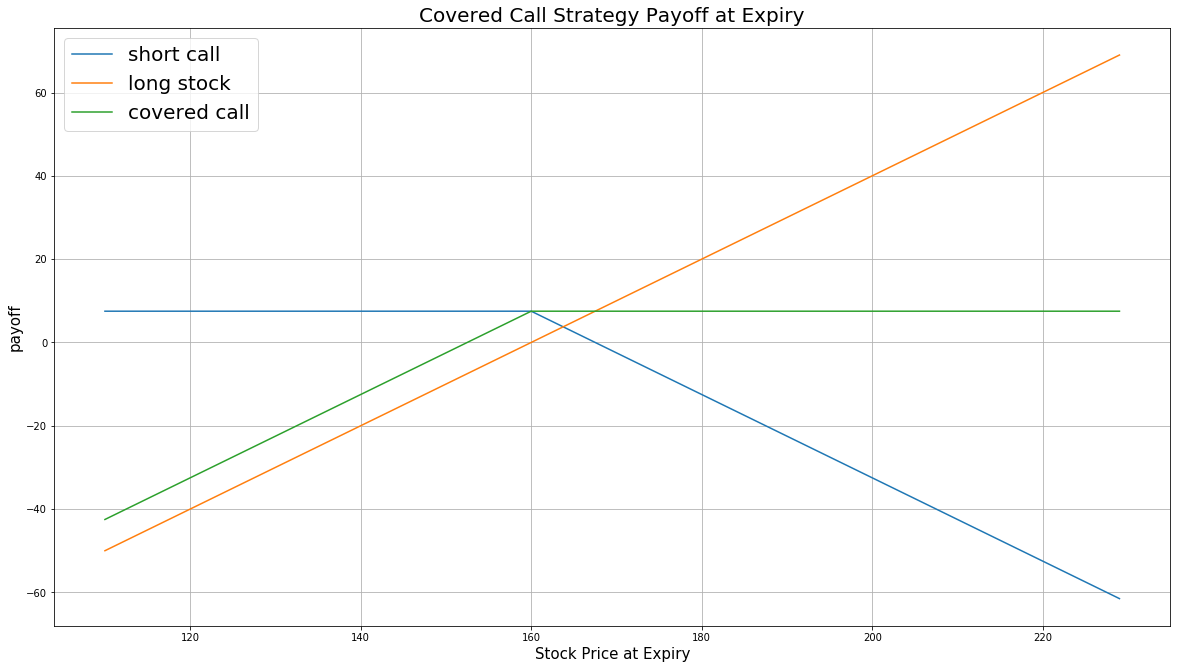
covered call strategy payoff

The maximum profit is $K - S_T + C^{K}_0$, which occurs when the underlying price is at or above the strike price of the call at expiration.

The maximum loss is $S_0 - C^{K}_0$, which ocurrs when the underlying price drops.

If the Option is American Option, there is a risk of early assignment on the contract you sell.

Example

The following table shows the price details of the assets in the algorithm:

AssetPrice ($)Strike ($)
Call3.35185.00
Underlying Equity at start of the trade187.07-
Underlying Equity at expiration190.01-

Therefore, the payoff is

$$ \begin{array}{rcll} C^{K}_T & = & (S_T - K)^{+}\\ & = & (190.01 - 185)^{+}\\ & = & 5.01\\ P_T & = & (S_T - S_0 + C^{K}_0 - C^{K}_T)\times m - fee\\ & = & (190.01 - 187.07 + 3.35 - 5.01)\times m - fee\\ & = & 1.28 \times 100 - 2\\ & = & 126 \end{array} $$

So, the strategy gains $126.

The following algorithm implements a covered call strategy:

You can also see our Videos. You can also get in touch with us via Discord.

Did you find this page helpful?

Contribute to the documentation: