Option Strategies

Long Put Butterfly

Introduction

Long Put butterfly is the combination of a bull put spread and a bear put spread. In this strategy, all the puts have the same underlying stock, the same expiration date, and the strike price distance of ITM-ATM and OTM-ATM put pairs are the same. The long put butterfly strategy consists of buying an ITM put, buying an OTM put, and selling 2 ATM puts. This strategy profits from low volatility.

Implementation

Follow these steps to implement the long put butterfly strategy:

  1. In the Initializeinitialize method, set the start date, end date, cash, and Option universe.
    2. private Symbol _symbol;

public override void Initialize()
{
    SetStartDate(2024, 9, 1);
    SetEndDate(2024, 12, 31);
    SetCash(500000);

    UniverseSettings.Asynchronous = true;
    var option = AddOption("GOOG", Resolution.Minute);
    _symbol = option.Symbol;
    option.SetFilter(universe => universe.IncludeWeeklys().PutButterfly(30, 5));
}
    def initialize(self) -> None:
    self.set_start_date(2024, 9, 1)
    self.set_end_date(2024, 12, 31)
    self.set_cash(500000)

    self.universe_settings.asynchronous = True
    option = self.add_option("GOOG", Resolution.MINUTE)
    self._symbol = option.symbol
    option.set_filter(lambda universe: universe.include_weeklys().put_butterfly(30, 5))

    The PutButterflyput_butterfly filter narrows the universe down to just the three contracts you need to form a long put butterfly.

  2. In the OnDataon_data method, select the contracts of the strategy legs.
    3. public override void OnData(Slice slice)
{
    if (Portfolio.Invested ||
        !slice.OptionChains.TryGetValue(_symbol, out var chain))
    {
        return;
    }

    // Select the call Option contracts with the furthest expiry
    var expiry = chain.Max(x =x> x.Expiry);    
    var puts = chain.Where(x => x.Expiry == expiry && x.Right == OptionRight.Put);
    if (puts.Count() == 0) return;

    // Select the ATM, ITM and OTM contracts from the remaining contracts
    var atmPut = puts.OrderBy(x => Math.Abs(x.Strike - chain.Underlying.Price)).First();
    var itmPut = puts.OrderBy(x => x.Strike).SkipLast(1).Last();
    var otmPut = puts.Single(x => x.Strike == atmPut.Strike * 2 - itmPut.Strike);
    def on_data(self, slice: Slice) -> None:
    if self.portfolio.invested:
        return

    # Get the OptionChain
    chain = slice.option_chains.get(self._symbol, None)
    if not chain:
        return

    # Get the furthest expiry date of the contracts
    expiry = max([x.expiry for x in chain])
    
    # Select the call Option contracts with the furthest expiry
    puts = [i for i in chain if i.expiry == expiry and i.right == OptionRight.PUT]
    if len(puts) == 0:
        return

    # Select the ATM, ITM and OTM contracts from the remaining contracts
    atm_put = sorted(puts, key=lambda x: abs(x.strike - chain.underlying.price))[0]
    itm_put = sorted(puts, key=lambda x: x.strike)[-2]
    otm_put = [x for x in puts if x.strike == atm_put.strike * 2 - itm_put.strike][0]
  3. In the OnDataon_data method, place the orders.

    4. Approach A: Call the OptionStrategies.ButterflyPutOptionStrategies.butterfly_put method with the details of each leg and then pass the result to the Buybuy method.

    var optionStrategy = OptionStrategies.ButterflyPut(_symbol, itmPut.Strike, atmPut.Strike, otmPut.Strike, expiry);
Buy(optionStrategy, 1);
    option_strategy = OptionStrategies.butterfly_put(self._symbol, itm_put.strike, atm_put.strike, otm_put.strike, expiry)
self.buy(option_strategy, 1)

    Approach B: Create a list of Leg objects and then call the Combo Market Ordercombo_market_order, Combo Limit Ordercombo_limit_order, or Combo Leg Limit Ordercombo_leg_limit_order method.

    var legs = new List<Leg>()
    {
        Leg.Create(atmPut.Symbol, -2),
        Leg.Create(itmPut.Symbol, 1),
        Leg.Create(otmPut.Symbol, 1)
    };
ComboMarketOrder(legs, 1);
    legs = [
    Leg.create(atm_put.symbol, -2),
    Leg.create(itm_put.symbol, 1),
    Leg.create(otm_put.symbol, 1)
]
self.combo_market_order(legs, 1)

Strategy Payoff

The long put butterfly is a limited-reward-limited-risk strategy. The payoff is

$$ \begin{array}{rcll} P^{OTM}_T & = & (K^{OTM} - S_T)^{+}\\ P^{ITM}_T & = & (K^{ITM} - S_T)^{+}\\ P^{ATM}_T & = & (K^{ATM} - S_T)^{+}\\ P_T & = & (P^{OTM}_T + P^{ITM}_T - 2\times P^{ATM}_T + 2\times P^{ATM}_0 - P^{ITM}_0 - P^{OTM}_0)\times m - fee \end{array} $$ $$ \begin{array}{rcll} \textrm{where} & P^{OTM}_T & = & \textrm{OTM put value at time T}\\ & P^{ITM}_T & = & \textrm{ITM put value at time T}\\ & P^{ATM}_T & = & \textrm{ATM put value at time T}\\ & S_T & = & \textrm{Underlying asset price at time T}\\ & K^{OTM} & = & \textrm{OTM put strike price}\\ & K^{ITM} & = & \textrm{ITM put strike price}\\ & K^{ATM} & = & \textrm{ATM put strike price}\\ & P_T & = & \textrm{Payout total at time T}\\ & P^{ITM}_0 & = & \textrm{ITM put value at position opening (debit paid)}\\ & P^{OTM}_0 & = & \textrm{OTM put value at position opening (debit paid)}\\ & P^{ATM}_0 & = & \textrm{ATM put value at position opening (credit received)}\\ & m & = & \textrm{Contract multiplier}\\ & T & = & \textrm{Time of expiration} \end{array} $$

The following chart shows the payoff at expiration:

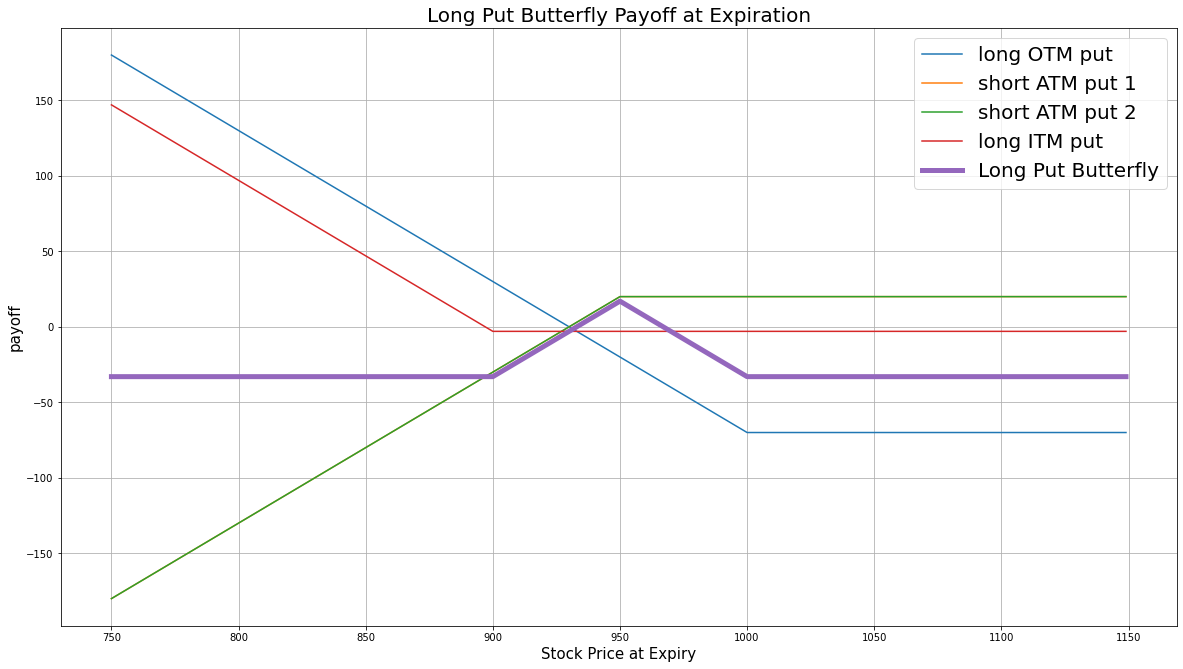
Strategy payoff decomposition and analysis of long put butterfly

The maximum profit is $K^{ATM} - K^{OTM} + 2\times P^{ATM}_0 - P^{ITM}_0 - P^{OTM}_0$. It occurs when the underlying price is the same at expiration as it was when you open the trade. In this case, the payout of the combined bull put and bear put spreads are at their maximum.

The maximum loss is the net debit paid, $2\times P^{ATM}_0 - P^{ITM}_0 - P^{OTM}_0$. It occurs when the underlying price is below the ITM strike price or above the OTM strike price at expiration.

If the Option is American Option, there is a risk of early assignment on the contracts you sell.

Example

The following table shows the price details of the assets in the long put butterfly algorithm:

AssetPrice ($)Strike ($)
ITM put37.80832.50
ATM put14.70800.00
OTM put5.70767.50
Underlying Equity at expiration829.08-

Therefore, the payoff is

$$ \begin{array}{rcll} P^{OTM}_T & = & (K^{OTM} - S_T)^{+}\\ & = & (829.08-832.50)^{+}\\ & = & 0\\ P^{ITM}_T & = & (K^{ITM} - S_T)^{+}\\ & = & (829.08-767.50)^{+}\\ & = & 61.58\\ P^{ATM}_T & = & (K^{ATM} - S_T)^{+}\\ & = & (829.08-800.00)^{+}\\ & = & 29.08\\ P_T & = & (P^{OTM}_T + P^{ITM}_T - 2\times P^{ATM}_T + 2\times P^{ATM}_0 - P^{ITM}_0 - P^{OTM}_0)\times m - fee\\ & = & (61.58+0-29.08\times2-5.70-37.80+14.70\times2)\times100-1.00\times4\\ & = & -1072 \end{array} $$

So, the strategy loses $1,072.

The following algorithm implements a long put butterfly Option strategy:

public class BearPutSpreadStrategy : QCAlgorithm
{
    private Symbol _equity;
    private Symbol _symbol;

    public override void Initialize()
    {
        SetStartDate(2024, 9, 1);
        SetEndDate(2024, 12, 31);
        SetCash(100000);

        _equity = AddEquity("GOOG", Resolution.Minute).Symbol;
        var option = AddOption("GOOG", Resolution.Minute);
        _symbol = option.Symbol;
        option.SetFilter(universe => universe.IncludeWeeklys().PutButterfly(30, 5));
    }

    public override void OnData(Slice slice)
    {
        if (Portfolio.Invested) return;

        // Get the OptionChain of the symbol
        var chain = slice.OptionChains.get(_symbol, null);
        if (chain == null || chain.Count() == 0) return;

        // sorted the optionchain by expiration date and choose the furthest date
        var expiry = chain.OrderByDescending(x => x.Expiry).First().Expiry;
        
        // filter the put options from the contracts which expire on the furthest expiration date in the option chain.
        var puts = chain.Where(x => x.Expiry == expiry && x.Right == OptionRight.Put);
        if (puts.Count() == 0) return;

        // sort the put options with the same expiration date according to their strike price.
        var putStrikes = puts.Select(x => x.Strike).OrderBy(x => x);

        // get at-the-money strike
        var atmStrike = puts.OrderBy(x => Math.Abs(x.Strike - chain.Underlying.Price)).First().Strike;

        // Get the distance between lowest strike price and ATM strike, and highest strike price and ATM strike. 
        // Get the lower value as the spread distance as equidistance is needed for both side.
        var spread = Math.Min(Math.Abs(putStrikes.First() - atmStrike), Math.Abs(putStrikes.Last() - atmStrike));

        // select the strike prices for forming the option legs
        var itmStrike = atmStrike + spread;
        var otmStrike = atmStrike - spread;

        var optionStrategy = OptionStrategies.PutButterfly(_symbol, itmStrike, atmStrike, otmStrike, expiry);
        // We open a position with 1 unit of the option strategy
        Buy(optionStrategy, 1);    // if long put butterfly
        //Sell(optionStrategy, 1);   // if short put butterfly
    }
}
class PutButterflyStrategy(QCAlgorithm): 
    def initialize(self) -> None:
        self.set_start_date(2024, 9, 1)
        self.set_end_date(2024, 12, 31)
        self.set_cash(500000)

        option = self.add_option("GOOG", Resolution.MINUTE)
        self.symbol = option.symbol
        option.set_filter(self.universe_func)

    def universe_func(self, universe: OptionFilterUniverse) -> OptionFilterUniverse:
        return universe.include_weeklys().put_butterfly(30, 5)

    def on_data(self, data: Slice) -> None:
        # avoid extra orders
        if self.portfolio.invested: return

        # Get the OptionChain of the self.symbol
        chain = data.option_chains.get(self.symbol, None)
        if not chain: return

        # sorted the optionchain by expiration date and choose the furthest date
        expiry = sorted(chain, key = lambda x: x.expiry, reverse=True)[0].expiry
        
        # filter the put options from the contracts which expire on the furthest expiration date in the option chain.
        puts = [i for i in chain if i.expiry == expiry and i.right == OptionRight.PUT]
        if len(puts) == 0: return

        # sort the put options with the same expiration date according to their strike price.
        put_strikes = sorted([x.strike for x in puts])

        # get at-the-money strike
        atm_strike = sorted(puts, key=lambda x: abs(x.strike - chain.underlying.price))[0].strike

        # Get the distance between lowest strike price and ATM strike, and highest strike price and ATM strike. 
        # Get the lower value as the spread distance as equidistance is needed for both side.
        spread = min(abs(put_strikes[0] - atm_strike), abs(put_strikes[-1] - atm_strike))

        # select the strike prices for forming the option legs
        itm_strike = atm_strike + spread
        otm_strike = atm_strike - spread

        option_strategy = OptionStrategies.put_butterfly(self.symbol, itm_strike, atm_strike, otm_strike, expiry)
        # We open a position with 1 unit of the option strategy
        self.buy(option_strategy, 1)
        # self.sell(option_strategy, 1) if short put butterfly

Other Examples

For more examples, see the following algorithms:

Demonstration Algorithm
IndexOptionPutButterflyAlgorithm.py Python IndexOptionPutButterflyAlgorithm.cs C#

You can also see our Videos. You can also get in touch with us via Discord.

Did you find this page helpful?

Contribute to the documentation: