Option Strategies

Protective Call

Introduction

A Protective Call consists of a short position in a stock and a long position in a call Option for the same amount of stock. Protective calls aim to hedge the short position of a stock with a long ATM or slightly OTM call Option. At any time for American Options or at expiration for European Options, if the stock moves below the strike price, the Option contract becomes worthless but the short position acquires an unrealized gain. If the underlying price moves above the strike, you can exercise the Options contract and receive the underlying Equity, which closes your short position.

Implementation

Follow these steps to implement the protective call strategy:

  1. In the Initializeinitialize method, set the start date, end date, cash, and Options universe.
    2. private Symbol _symbol;

public override void Initialize()
{
    SetStartDate(2024, 9, 1);
    SetEndDate(2024, 12, 31);
    SetCash(100000);

    UniverseSettings.Asynchronous = true;
    var option = AddOption("IBM");
    _symbol = option.Symbol;
    option.SetFilter(universe => universe.IncludeWeeklys().NakedCall(30, 0));
}
    def initialize(self) -> None:
    self.set_start_date(2024, 9, 1)
    self.set_end_date(2024, 12, 31)
    self.set_cash(100000)

    self.universe_settings.asynchronous = True
    option = self.add_option("IBM")
    self._symbol = option.symbol
    option.set_filter(lambda universe: universe.include_weeklys().naked_call(30, 0))

    The NakedCallnaked_call filter narrows the universe down to just the one contract you need to form a protective call.

  2. In the OnDataon_data method, select the Option contract.
    3. public override void OnData(Slice slice)
{
    if (Portfolio.Invested ||
        !slice.OptionChains.TryGetValue(_symbol, out var chain)) return;

    // Find ATM call with the farthest expiry
    var expiry = chain.Max(x => x.Expiry);
    var atmCall = chain
        .Where(x => x.Right == OptionRight.Call && x.Expiry == expiry)
        .OrderBy(x => Math.Abs(x.Strike - chain.Underlying.Price))
        .FirstOrDefault();
    def on_data(self, slice: Slice) -> None:
    if self.portfolio.invested:
        return

    chain = slice.option_chains.get(self._symbol)
    if not chain:
        return

    # Find ATM call with the farthest expiry
    expiry = max([x.expiry for x in chain])
    call_contracts = sorted([x for x in chain
        if x.right == OptionRight.CALL and x.expiry == expiry],
        key=lambda x: abs(chain.underlying.price - x.strike))

    if not call_contracts:
        return

    atm_call = call_contracts[0]
  3. In the OnDataon_data method, place the orders.

    4. Approach A: Call the OptionStrategies.ProtectiveCallOptionStrategies.protective_call method with the details of each leg and then pass the result to the Buybuy method.

    var protectiveCall = OptionStrategies.ProtectiveCall(_symbol, atmCall.Strike, expiry);
Buy(protectiveCall, 1);
    protective_call = OptionStrategies.protective_call(self._symbol, atm_call.strike, expiry)
self.buy(protective_call, 1)

    Approach B: Create a list of Leg objects and then call the Combo Market Ordercombo_market_order, Combo Limit Ordercombo_limit_order, or Combo Leg Limit Ordercombo_leg_limit_order method.

    var legs = new List<Leg>()
    {
        Leg.Create(atmCall.Symbol, 1),
        Leg.Create(chain.Underlying.Symbol, -chain.Underlying.SymbolProperties.ContractMultiplier)
    };
ComboMarketOrder(legs, 1);
    legs = [
    Leg.create(atm_call.symbol, 1),
    Leg.create(chain.underlying.symbol, -chain.underlying.symbol_properties.contract_multiplier)
]
self.combo_market_order(legs, 1)

Strategy Payoff

The payoff of the strategy is

$$ \begin{array}{rcll} C^{K}_T & = & (S_T - K)^{+}\\ P_T & = & (S_0 - S_T + C^{K}_T - C^{K}_0)\times m - fee \end{array} $$ $$ \begin{array}{rcll} \textrm{where} & C^{K}_T & = & \textrm{Call value at time T}\\ & S_T & = & \textrm{Underlying asset price at time T}\\ & K & = & \textrm{Call strike price}\\ & P_T & = & \textrm{Payout total at time T}\\ & S_0 & = & \textrm{Underlying asset price when the trade opened}\\ & C^{K}_0 & = & \textrm{Call price when the trade opened (credit received)}\\ & m & = & \textrm{Contract multiplier}\\ & T & = & \textrm{Time of expiration} \end{array} $$

The following chart shows the payoff at expiration:

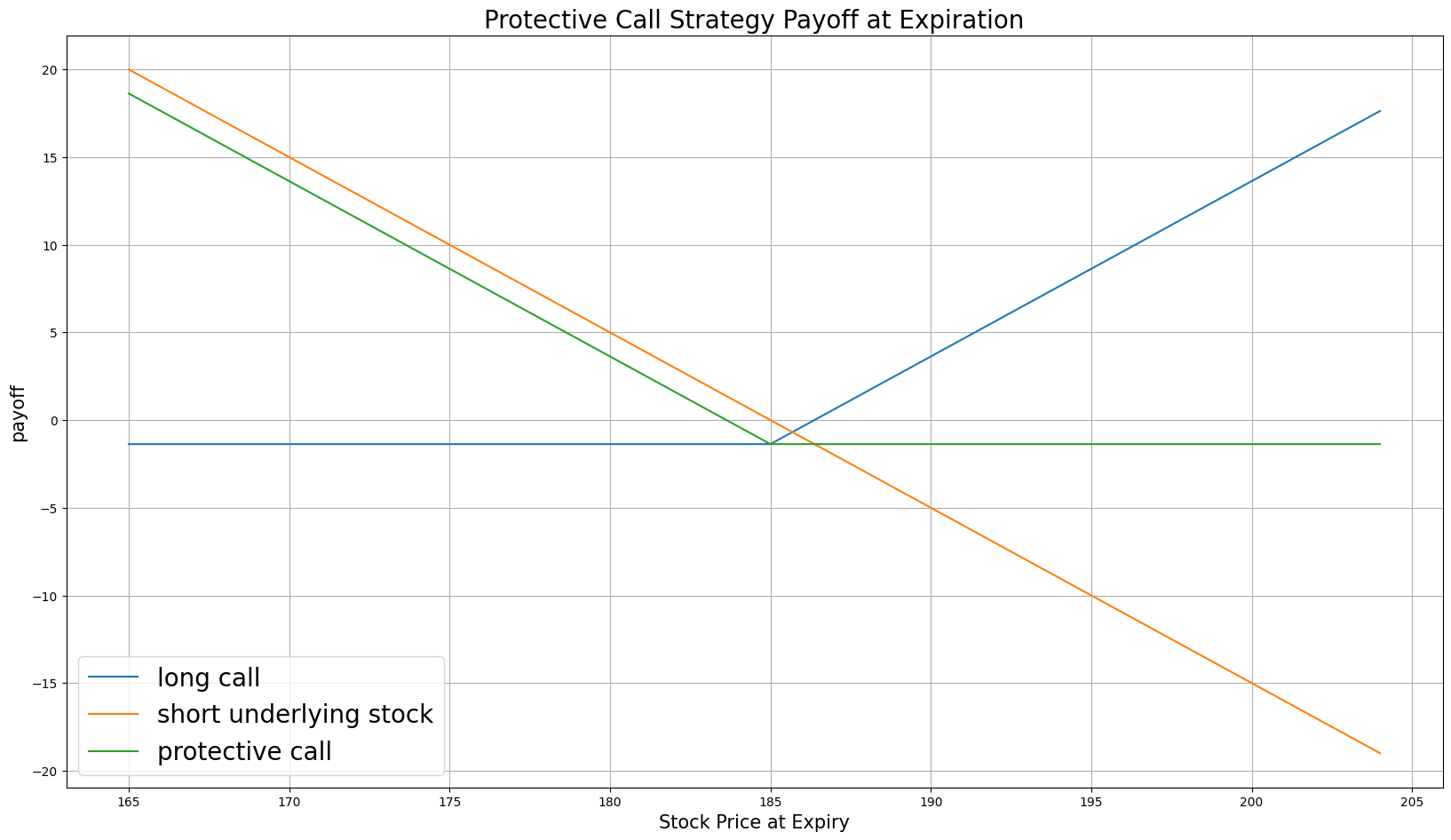
Strategy payoff decomposition and analysis of protective call

The maximum profit is $S_0 - C^{K}_0$, which occurs when the underlying price is $0$.

The maximum loss is $S_0 - K - C^{K}_0$, which occurs when the underlying price is above the strike price.

Example

The following table shows the price details of the assets in the algorithm:

AssetPrice ($)Strike ($)
Call3.50185.00
Underlying Equity at start of the trade186.94-
Underlying Equity at expiration190.01-

Therefore, the payoff is

$$ \begin{array}{rcll} C^{K}_T & = & (S_T - K)^{+}\\ & = & (190.01 - 185)^{+}\\ & = & 5.01\\ P_T & = & (S_0 - S_T + C^{K}_T - C^{K}_0)\times m - fee\\ & = & (186.94 - 190.01 + 5.01 - 3.50)\times m - fee\\ & = & -1.56 \times 100 - 2\\ & = & -158 \end{array} $$

So, the strategy loses $158.

The following algorithm implements a protective call Option strategy:

public class ProtectiveCallAlgorithm : QCAlgorithm
{
    private Symbol _call, _symbol;
    
    public override void Initialize()
    {
        SetStartDate(2024, 9, 1);
        SetEndDate(2024, 12, 31);
        SetCash(100000);

        var option = AddOption("IBM");
        _symbol = option.Symbol;
        option.SetFilter(universe => universe.IncludeWeeklys().NakedCall(30, 0));

        // use the underlying equity as the benchmark
        SetBenchmark(_symbol.Underlying);
    }

    public override void OnData(Slice slice)
    {
        if (_call != null && Portfolio[_call].Invested) return;

        if (!slice.OptionChains.TryGetValue(_symbol, out var chain)) return;

        // Find ATM call with the farthest expiry
        var expiry = chain.Max(x => x.Expiry);
        var atmCall = chain
            .Where(x=> x.Right == OptionRight.Call && x.Expiry == expiry)
            .OrderBy(x => Math.Abs(x.Strike - chain.Underlying.Price))
            .FirstOrDefault();

        if (atmCall == null) return;

        var protectiveCall = OptionStrategies.ProtectiveCall(_symbol, atmCall.Strike, expiry);
        Buy(protectiveCall, 1);

        _call = atmCall.Symbol;
    }
}
class ProtectiveCallAlgorithm(QCAlgorithm):
    def initialize(self) -> None:
        self.set_start_date(2024, 9, 1)
        self.set_end_date(2024, 12, 31)
        self.set_cash(100000)

        option = self.add_option("IBM")
        self.symbol = option.symbol
        option.set_filter(lambda universe: universe.include_weeklys().naked_call(30, 0))

        self.call = None

        # use the underlying equity as the benchmark
        self.set_benchmark(self.symbol.underlying)

    def on_data(self, slice: Slice) -> None:
        if self.call and self.portfolio[self.call].invested:
            return

        chain = slice.option_chains.get(self.symbol)
        if not chain:
            return

        # Find ATM call with the farthest expiry
        expiry = max([x.expiry for x in chain])
        call_contracts = sorted([x for x in chain
            if x.right == OptionRight.CALL and x.expiry == expiry],
            key=lambda x: abs(chain.underlying.price - x.strike))

        if not call_contracts:
            return

        atm_call = call_contracts[0]

        protective_call = OptionStrategies.protective_call(self.symbol, atm_call.strike, expiry)
        self.buy(protective_call, 1)

        self.call = atm_call.symbol

You can also see our Videos. You can also get in touch with us via Discord.

Did you find this page helpful?

Contribute to the documentation: